Electron Propagator Calculations of Vertical Electron Binding Energies and Dyson Orbitals in Gaussian 16

Filip Pawłowski and J. V. Ortiz

Electron propagator theory (EPT) is used for ab initio calculations of vertical electron binding energies (VEBEs) of atoms, molecules and ions, e.g.,

vertical ionization potentials (VIPs) of molecules (example input and output),
vertical electron affinities (VEAs) of molecules (example input and output),
vertical electron detachment energies (VEDEs) of anions (example input and output),
ground-state and excited-state energies of radicals inferred from vertical electron attachment energies (VEAEs) of cations (example input and output).

In addition, EPT is used to determine Dyson orbitals. A Dyson orbital is a generalization of a frozen, Hartree-Fock canonical molecular orbital (CMO) that is modified by the effects of orbital relaxation and electron correlation.

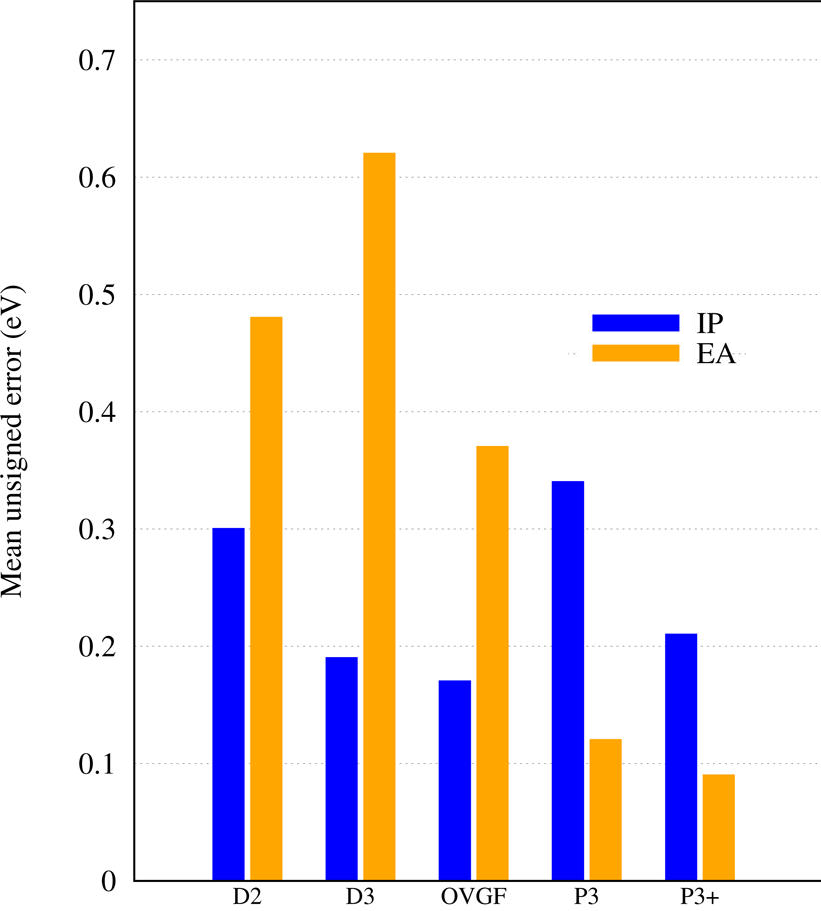
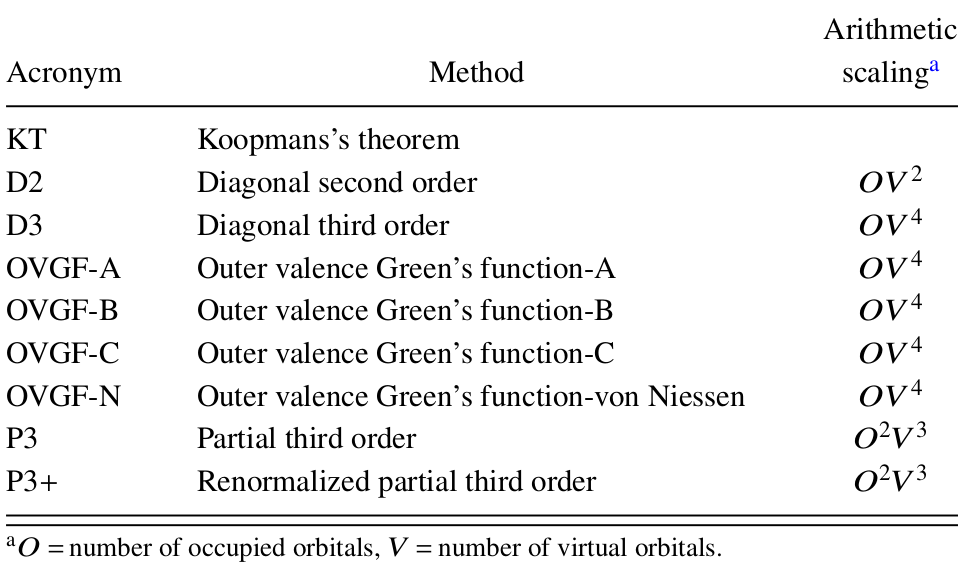
EPT methods start with the simple Koopmans's theorem (KT) result and systematically improve upon it to approach exact VEBEs. This strategy differs from density-functional theory (DFT) and resembles that of wave-function theory (WFT) methods. An advantage of EPT over evaluation of total energies for initial and final states with WFT (e.g. ΔMP2, ΔCCSD(T)) is calculating VEBEs directly. Unlike many direct WFT methods, such as EOM-CCSD, EPT calculations yield a single Dyson orbital for each VEBE.

In general, the P3+ and NR2 EPT methods have a computational cost comparable to and accuracy surpassing second-order Møller-Plesset perturbation theory (MP2). Several final states are usually accessible; final-state excitation energies may be inferred from differences of VEBEs.

(Arithmetic scaling below refers to IPs; click on the figure or table to enlarge.)

Previous version of this tutorial (for Gaussian 09 users)

References

Second order [1-3]
Third order [4]
Partial third order (P3) [5, 6]
Renormalized partial third order (P3+) [7, 8]
Outer Valence Green Function (OVGF) [9-12]
Two-particle-hole Tamm-Dancoff approximation (2ph-TDA) [13, 14]
Renormalized third order (3+) [12]
Third order algebraic diagrammatic contruction (ADC3) [15, 16]
Nondiagonal renormalized second order (NR2) [17, 18]
EPT reviews [8, 12, 18-25]
Algorithms [19, 26-28]
General references [29, 30]

[1] D.J. Thouless, The Quantum Mechanics of Many-Body Systems, Academic Press, New York, 1961.
[2] W.P. Reinhardt, J.D. Doll, Direct Calculation of Natural Orbitals by Many‐Body Perturbation Theory: Application to Helium, J. Chem. Phys. 50 (1969) 2767-2768.
[3] J.D. Doll, W.P. Reinhardt, Many-body Green's functions for finite, nonuniform systems. Applications to closed-shell atoms, J. Chem. Phys. 57 (1972) 1169-1184.
[4] L.S. Cederbaum, Direct calculation of ionization potentials of closed-shell atoms and molecules, Theor. Chim. Acta 31 (1973) 239-260.
[5] J.V. Ortiz, Partial third-order quasiparticle theory: comparisons for closed-shell ionization energies and an application to the Borazine photoelectron spectrum, J. Chem. Phys. 104 (1996) 7599-7605.
[6] A.M. Ferreira, G. Seabra, O. Dolgounitcheva, V.G. Zakrzewski, J.V. Ortiz, Application and testing of diagonal, partial third-order electron propagator approximations, Understanding Chem. React. 22 (2001) 131-160.
[7] J.V. Ortiz, An efficient, renormalized self-energy for calculating the electron binding energies of closed-shell molecules and anions, Int. J. Quantum Chem. 105 (2005) 803-808.
[8] J.V. Ortiz, Electron propagator theory: an approach to prediction and interpretation in quantum chemistry, Wiley Interdisciplinary Reviews: Computational Molecular Science 3 (2013) 123-142.
[9] L.S. Cederbaum, One-body Green's function for atoms and molecules. Theory and application, J. Phys. B 8 (1975) 290-303.
[10] W. von Niessen, J. Schirmer, L.S. Cederbaum, Computational methods for the one-particle Green's function, Comput. Phys. Rep. 1 (1984) 57-125.
[11] V.G. Zakrzewski, J.V. Ortiz, J.A. Nichols, D. Heryadi, D.L. Yeager, J.T. Golab, Comparison of perturbative and multiconfigurational electron propagator methods, Int. J. Quantum Chem. 60 (1996) 29-36.
[12] J.V. Ortiz, The electron propagator picture of molecular electronic structure, Comput. Chem. Rev. Current Trends 2 (1997) 1-61.
[13] L.S. Cederbaum, W. Domcke, Theoretical aspects of ionization potentials and photoelectron spectroscopy: a Green's function approach, Adv. Chem. Phys. 36 (1977) 205-344.
[14] J. Schirmer, L.S. Cederbaum, The two-particle-hole Tamm-Dancoff approximation (2ph-TDA) equations for closed-shell atoms and molecules, J. Phys. B 11 (1978) 1889-1900.
[15] J. Schirmer, L.S. Cederbaum, O. Walter, New approach to the one-particle Green's function for finite Fermi systems, Physical Review A 28 (1983) 1237-1259.
[16] J. Schirmer, G. Angonoa, On Green-function calculations of the static self-energy part, the ground state energy, and expectation values, J. Chem. Phys. 91 (1989) 1754-1761.
[17] J.V. Ortiz, A nondiagonal, renormalized extension of partial third-order quasiparticle theory: comparisons for closed-shell ionization energies, J. Chem. Phys. 108 (1998) 1008-1014.
[18] H.H. Corzo, J.V. Ortiz, Electron Propagator Theory: Foundations and Predictions, Adv. Quantum Chem. 74 (2017) 267-298.
[19] J.V. Ortiz, V.G. Zakrzewski, O. Dolgounitcheva, One-electron pictures of electronic structure: propagator calculations on photoelectron spectra of aromatic molecules, in: J.-L. Calais, E. Kryachko (Eds.), Conceptual Perspectives in Quantum Chemistry, Kluwer, Dordrecht, 1997, pp. 465-517.
[20] J.V. Ortiz, Toward an exact one-electron picture of chemical bonding, Adv. Quantum Chem. 35 (1999) 33-52.
[21] R. Flores-Moreno, J. Melin, O. Dolgounitcheva, V.G. Zakrzewski, J.V. Ortiz, Three approximations to the nonlocal and energy-dependent correlation potential in electron propagator theory, Int. J. Quantum Chem. 110 (2010) 706-715.
[22] V.G. Zakrzewski, O. Dolgounitcheva, A.V. Zakjevskii, J.V. Ortiz, Ab initio electron propagator methods: applications to fullerenes and nucleic acid fragments, Annu. Rep. Comput. Chem. 6 (2010) 79-94.
[23] R. Flores-Moreno, J.V. Ortiz, Efficient and Accurate Electron Propagator Methods and Algorithms, in: J. Leszczynski, M.K. Shukla (Eds.), Practical Aspects of Computational Chemistry: Methods, Concepts and Applications, Springer Netherlands, Dordrecht, 2010, pp. 1-17.
[24] V.G. Zakrzewski, O. Dolgounitcheva, A.V. Zakjevskii, J.V. Ortiz, Ab initio electron propagator calculations on electron detachment energies of fullerenes, macrocyclic molecules, and nucleotide fragments, Adv. Quantum Chem. 62 (2011) 105-136.
[25] J.V. Ortiz, Interpreting Bonding and Spectra With Correlated, One-Electron Concepts From Electron Propagator Theory, Annu. Rep. Comput. Chem. 13 (2017) 139-182.
[26] V.G. Zakrzewski, J.V. Ortiz, Semidirect algorithms in electron propagator calculations, Int. J. Quantum Chem., Quantum Chem. Symp. 28 (1994) 23-27.
[27] V.G. Zakrzewski, J.V. Ortiz, Semidirect algorithms for third-order electron propagator calculations, Int. J. Quantum Chem. 53 (1995) 583-590.
[28] V.G. Zakrzewski, O. Dolgounitcheva, J.V. Ortiz, Improved algorithms for renormalized electron propagator calculations, Int. J. Quantum Chem. 75 (1999) 607-614.
[29] J. Linderberg, Y. Öhrn, Propagators in Quantum Chemistry, Second Edition, Wiley-Interscience, Hoboken NJ, 2004.
[30] P. Jørgensen, J. Simons, Second Quantization-Based Methods in Quantum Chemistry, Academic Press, New York, 1981.