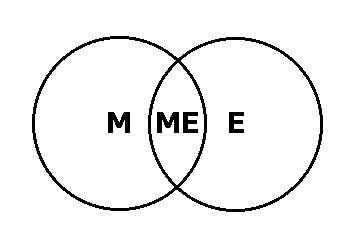Mises and His Methods

Roger W. Garrison*
 

Over the past several years, I have participated in a number of short courses on Austrian economics, and for some I was involved in the planning stages. The one aspect of such planning that stands out in my memory has to do with the issue of methodology. How should we present the methodological precepts that underlie Austrian theory? There seemed to be three possibilities: We could deal head-on with the methodological issues in the first lecture, in which case we would spend the remainder of the course trying to put methodology behind us in order to deal with the substantive issues; we could postpone discussion of methodology to the very end, in which case we would spend most of the course anticipating the arguments to be presented in that last lecture; or we could simply exclude methodology from our schedule of lectures, in which case every lecture that we did schedule would quickly transform itself into a discussion of the methodological underpinnings.
        I have some concern that my present discussion of Mises and his methods may propel me into the "black hole of methodology." Economists who allow themselves to become totally immersed in methodological issues rarely escape to do substantive work. In an attempt to keep one foot outside of the black hole, I propose to steer clear of the loftier issues of metaphysics, epistemology, and philosophy of science. I will deal instead with the workaday methods used by Mises and by those who have followed his lead. How did Mises go about doing economics? How do his methods compare with those of the modern mainstream?
        The issues have become standard: the appropriateness of mathematical formulations, the relationship between theory and statistical data, and the role of assumptions in economic theorizing. Recent developments in econometric methods and in mathematical modeling techniques allow the contrast between Mises and the more modern practitioners to be sharpened. 

I. Mathematical Economics and the Eclipse of Causality
Appearing two years before the initial publication of Mises's Human Action (1949) was Paul Samuelson's Foundations of Economic Analysis (1947), the title page adorned with a pronouncement by J. Willard Gibbs: "Mathematics is a Language." Samuelson mastered that language in the course of his training at the University of Chicago and then at Harvard. According to Fischer [1987, p. 234], "Samuelson more than anyone else brought economics from its pre-1930s verbal and diagrammatic mode of analysis to the quantitative mathematical style and methods of reasoning that have dominated for the last three decades." The techniques of the physical sciences are so dominant today that an economist who prefers not to use mathematics in his economic theorizing is held in the same regard as a sculptor who prefers not to use a chisel or a welder who prefers not to use a torch.
        Economists who choose to work within the tradition begun by Menger and firmly established by Mises may be tempted to take issue directly with Willard Gibbs. But there is no justification for insisting upon a narrow conception of language. Mathematics is a language. We can respond to Samuelson in a more telling way with the claim that so too is music. There is no reason for economists to observe a categorical prohibition against either mathematical formulation or musical expression. The relevant question is: What sort of language�music, mathematics, or, say, English�allows economists best to communicate their ideas? Which language serves the economist without imposing constraints of its own upon his subject matter?
        The answer to the question just posed depends, of course, upon what the economist takes his subject matter to be. And in particular the answer turns�both for Mises and for modern mathematical economists�on whether or not causality in economics is a worthy concern. For Mises causality was the central concern. His methodological individualism has as its goal the establishment of a causal linking of individual actions to observed economic phenomena. The very title of Mises's magnum opus identifies his starting point. Human action is the root cause of all economic phenomena. The task of the economist, in Mises's view, is to draw out the historically relevant implications of the fact that individuals act�that they employ means to achieve ends. Alternatively stated, the economist's task is to devise a logic of action�a praxeology, to use the Misesian term.⁽¹⁾
        For Mises and the Austrians, cause and effect in economic theory manifest themselves as human action and its consequences. By human action Mises simply meant purposeful behavior; by consequences he included both the intended consequences and the unintended consequences but maintained a sharp distinction between the two categories. Many of his theories, in fact, involved a contrast between the intentions of market participants or policy makers and actual consequences that flow from the market process.
        Systems of equations can be suitably employed to describe the consequences of human action, but such mathematical descriptions are inherently blind to notions of intentionality and causality. In the words of Mises [1966, p. 356], "[The] equations and formulas [of mathematical economics] are limited to the description of states of equilibrium and nonacting." Until recently, mathematical economists saw the eclipse of causality as one of the virtues of the mathematical method. Four decades ago, for instance, George Stigler [1946, p. 181] wrote approvingly that the profession had abandoned the "older concept of cause and effect" in favor of the "concepts of mutual determination" and accused those still concerned with causality with "fail[ing] to understand some of the most essential elements of modern... theory."⁽²⁾
        Philosophical insight into the meaning of causality is not at issue here. The point is that some modes of expression make nonsense out of the question of cause and effect. An orange�or other spheroid�placed in a large rounded bowl will come to rest at the very center of the bowl. Gravity, we might be inclined to say, is the "cause" of this result. But suppose that two oranges are placed in the bowl. Which one of the oranges causes the other to be displaced from the center? The question itself is nonsensical. We can describe the loci of possible resting points of the two oranges, however, by manipulating the mathematical expressions representing the sizes and shapes of the oranges and the bowl. The two points of contact, of course, would be mutually determined.
        In economics, it is possible to phrase questions about causality which are equally�but maybe not obviously�nonsensical. Under a variety of circumstances, real wage rates and real interest rates are inversely related to one another. But does a low interest rate cause the wage rate to be high, or does a high wage rate cause the interest rate to be low? The question simply makes no sense; the two rates are analogous to the two resting points of the oranges.
        This particular example of the eclipse of causality is not a frivolous one. The inverse relationship between the wage rate and the interest rate forms the bedrock of Ricardian distribution theory.⁽³⁾ For neo-Ricardians who adopted the mathematical method, the question of which rate was the cause and which the effect gave way to the question of which rate is "exogenous" to the relationship, or predetermined, and which is "endogenous," or determined by the relationship? Those who believed that the interest rate is predetermined (by social convention) became Cambridge capital theorists; those who believed that the wage rate is predetermined (by the requirements for subsistence) became Marxists. Agnosticism about the true locus of exogeneity was also a respectable position�one that provided a half-way house for neo-Ricardians making a conversion in one direction or the other.
        Mathematics can describe the various combinations of wage and interest rates but cannot answer or even make sense of questions about which caused which or about which one is, in reality, determined exogenously. The mathematical economist, however, is content to remain agnostic on the issue of causality; the two rates are mutually determined. The praxeologist, by contrast, seeks to identify the plans and actions of individuals in the marketplace which constitute the ultimate cause of the pattern of wage and interest rates.
        While mathematical economists may not deny that the ultimate cause is to be found in the actions of market participants, they proceed untroubled by the fact that mathematics is inherently silent on the issue of cause and effect. This disadvantage of the mathematical method was Mises's concern [1966, p. 350] when he remarked that "[i]ts syllogisms are not only sterile; they divert the mind from the study of the real problems and distort the relationships between the various phenomena."
        The claim is sometimes made that any relationship, including presumably causal relationships, can be expressed mathematically. John Egger's attempt to give plausibility to this claim by offering a far-fetched example is noteworthy because the particular example he chose provides, if only inadvertently, a sound basis for rejecting the claim. Egger [1978, p. 29] translates the old saw "absence makes the heart grow fonder" into f'(x)>0. (The first derivative of fondness with respect to absence is greater than zero.) Tellingly, the word "makes," which indicates the direction of causality, is unavoidably lost in the translation. The exact same mathematical expression would result from a translation of the converse: "growing fonder makes the heart absent."
        At best, Egger's equation can describe the equilibrium relationship between "absence" and the "growth rate of fondness." More likely, however, such a wanton use of mathematics would invite attempts to quantify inherently unquantifiable concepts. And worse, the very fact that the expression involves a derivative suggests the appropriateness of the calculus operators. Egger could hardly argue against those who might want to integrate the equation in order to determine the absolute level of fondness that corresponds to an absence of a given duration. The real lesson in his curious exercise is not that any idea can be expressed mathematically but rather that mathematical economists have tortured economics in the same way that Egger has tortured a piece of romantic prose.

II. "Causality" in Modern Empirical Economics
Considerations of technique prevent the modern economist from addressing the full range of economic questions. As mathematician, he can shed no light on issues of causality, but as economist, he is continually confronted with such issues. The melding of classical statistics with formal mathematical modeling, which establishes a link between theoretical abstractions and historical experience, does not close the gap between issues and answers. All respectable texts on statistics and econometrics acknowledge that statistical inference can never identify cause and effect; they warn against interpreting correlation as causation.
        In recent years it has become acceptable within the economics profession to ignore all such acknowledgments and warnings and to make claims about cause and effect on the basis of empirical tests. For a hypothetical example, the claim that a rising interest rate causes the wage rate to fall may be supported by time-series analysis in which an inverse relationship between wage rates and lagged interest rates is demonstrated. The long-respected strictures against reading causality into statistical patterns are flouted. Empirical causality tests are increasingly common in the professional literature.
        Only in the early phase of this empirical innovation was it made clear that such tests are based upon a newly stipulated definition of the word "cause." Stripped of all its subtle and difficult philosophical content and of its etymological link with reason, the word "cause" is used to describe observed temporal patterns in time-series data. In the judgment of Clive Granger and Paul Newbold [1977. p. 225], "A better term might be temporally related, but since cause is such a simple term we shall continue to use it." It is interesting to note that, though this usage is defended on the basis of simplicity of expression, economists who employ empirical techniques developed by Granger use the decidedly unsimple and unaesthetic term "Granger-cause," as in: Falling interest rates Granger-cause wage rates to rise.
        Christopher Sims, most widely known for his development and use of techniques suggested by Granger, is explicit about the nature of his enterprise. "The method of identifying causal direction employed here does rest on a sophisticated version of the post hoc ergo propter hoc principle" [1972, p. 543]. "After this, therefore because of this," of course, is not a principle at all, but a fallacy. And sophistication cannot convert fallacy into principle.
        The linguistic technique introduced by Granger is nothing short of a scandal. (A better term might be career enhancing innovation, but since scandal is such a simple term I shall continue to use it.) Publishers and editors are not likely to be interested in research that yields limp conclusions about the temporal relationships in the movements of economic variables; they are interested in research that demonstrates that one thing causes another.
        Granger-inspired research is often reported guardedly in the section on the testing procedure and then unguardedly in the summary section. Gerald P. Dwyer, Jr. [1982], for instance, conducts Granger-causality tests to determine whether or not federal budget deficits Granger-cause inflation. Failing to find any statistically significant post-hoc relationship, he tentatively reports in his summary that "...there is no reason to predict that a reduction of deficits has a causal role in any policy to reduce inflation."
        The economist's audience is interested in the issue of causality; his mathematical and econometric techniques are not up to the task. The result�for those who confine themselves to mathematical and statistical methods�is a scandalous abuse of the English language. For Mises the notion of cause and effect as used by economists is presupposed by the notion of means and ends, where both cause and means are to be understood in terms of the purposes and plans of acting individuals. None of these notions are adequately illuminated by the methods of mathematical economists or econometricians. 

III. Mathematical Economics in Perspective
To recognize that the notion of causality cannot be expressed mathematically or tested-for empirically is to suggest that, for the economist, the language of mathematics and econometrics is too confining. Systems of equations can be used to describe abstract states of general equilibrium, and econometrics can provide some quantification of actual economic magnitudes. There should be no objection to this.⁽⁴⁾ In fact, the appropriateness of mathematics for describing an economy in general equilibrium or for describing the evenly rotating economy, to use Mises's own construction, derives precisely from the fact that there is no human action in such states. The Austrian economist, however, is interested primarily in the give and take of market processes. This is where the action is. But his task of making those processes intelligible by identifying the plans and actions that give rise to them is not facilitated by the mathematical method.
        There is no justification for insisting that mathematical formulations be expunged from economics in some wholesale fashion. The appropriate imperative is much milder in both substance and tone: Do not allow the applicability of mathematical and statistical methods to define the scope of economics. Most economists if confronted explicitly with this recommendation would, I suspect, accept it, many believing that it simply goes without saying. Implicitly, however, the recommendation is systematically rejected�as judged by the extent to which the applicability of these methods have in fact been allowed to dictate subject matter.
        It is convenient to describe the current state of economics with the aid of a simple Venn diagram consisting of two overlapping circles (see Figure 1). Let one circle M represent mathematics; let the other E represent economics. The overlap ME represents mathematical economics and includes all those aspects of economics that actually are�even in the Austrian view�susceptible to a mathematical treatment. Descriptions of equilibrium states, for instance, fall in this overlap. Mises's only complaint about such exercises [1966, p. 355] is that they have unduly dominated the attention of economists: "A superficial analogy [i.e. the imaginary construction of the final state of rest translated into algebraic symbols] is spun out too long...."
 

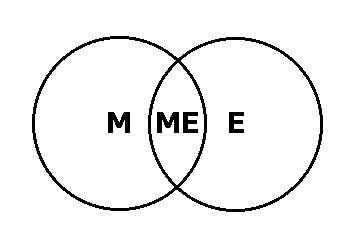
Figure 1: Venn Diagram

         The very construction of the Venn diagram suggests that economists who use the mathematical method should take precautions of two sorts. First, they should guard against allowing mathematical exercises to take them across the border separating M from ME, where the equations cease to express relationships having any relevance to economics. Second, they should strive continuously to maintain free passage across the other border, which separates ME from E. They should willingly make excursions into any area of economics�even if they have to abandon the vehicle of mathematics at the border. Anyone familiar with today's economics profession will quickly realize that the border guards are misdeployed. Dissatisfaction with the state of the profession stems largely, I think, from the work of economists who are oblivious to the border that should not be crossed but who instinctively retreat from the border that should be ignored.
        The professional journals are filled with technically sophisticated articles in which mathematical formulations and manipulations have no clear relevance to economic reality. The problem is not abstractness per se. The most fundamental and broadly applicable propositions of economics are inherently abstract. Nor is the realism of assumptions directly at issue here.⁽⁵⁾ The problem is the failure to maintain a distinction between mathematical economics and mathematical gymnastics.
        Charles L. Schultze [as quoted by Herron, 1987] recognized the problem of the unguarded border in his assessment of modern technical economics. The profession tends to engage itself in what Schultze calls "finger exercises�you can't tell where the mathematics ends and the economics begins." More typically, the crossing of the unguarded border occurs in the opposite direction (i.e., from ME into M) from that suggested by Schultze's lament. Mathematical economists begin by associating their symbols with economic magnitudes: k is capital; l is labor; q is output, etc. They proceed, then, to manipulate mathematical equations without concern about the economic meaningfulness�or the possible meaninglessness�of the resulting relationships.
        One of the clearest examples of this mathematical procedure is the infamous Cambridge Controversy over capital and the production function. Polynomials that purportedly described multiperiod production processes yielded pro forma solutions suggesting the possible existence of multiple pure rates of interest, technique reswitching, and capital reversing. Without question these odd-sounding phrases were descriptive of the mathematical results obtained by Cambridge capital theorists; but they are not meaningful in the context of any known economic process. Demonstrations that the results have economic significance are nonexistent, and even the recognition of this lacking is less than sincere. The final sentence of an article on capital reswitching appearing in the profession's most prestigious journal reads: "What now remains is to establish the economic significance of the constraints imposed to allow us to get these results" [Galloway and Shukla, 1974, p. 358]. But more than a decade later, that task, which should have been preliminary to the publication of the mathematical results, still remains. The results themselves have become and continue to be the subject matter of further study.⁽⁶⁾
        The problem of the unguarded border is compounded by a problem of the opposite sort on the other side of the overlap. It has become standard practice in the profession today to make assumptionssometimes bizarre assumptions�in order to render an economic issue mathematically tractable, i.e., to avoid crossing from ME into E. An analysis of the give-and-take of the market process is often precluded or trivialized by some assumption that focuses attention on the end result of that process. Examples of assumptions that guard against plunging head-long into non-mathematical economics are easy to find. The Walrasian auctioneer has come to serve as one such border guard. Invoking this piece of fiction allows the mathematical economist to pass over the question of how the economy actually gropes towards an equilibrium and to neglect the consequences of transactions involving disequilibrium prices. A single auctioneer substitutes for competing entrepreneurs, making it unnecessary for market participants to engage in monetary calculation in any nontrivial way or to formulate and implement economic plans. All the issues that captured the attention of Mises and the Austrians are held at bay while the mathematical economists describe the pattern of prices and the allocation of resources associated with a general equilibrium.
        The Friedmanian helicopter does for monetary theory what the Walrasian auctioneer does for value theory. Mathematical tractability is preserved if it can be assumed that monetary injections are accomplished by helicopter drops of newly created money. It is often further assumed in the Monetarist literature that individuals gather up the new money in direct proportion to the amount that they already possess. Propositions about the neutrality of money follow trivially: production functions are homogeneous of degree zero with respect to the medium of exchange. Again, the issues of interest to the Austrians�injection effects, monetary distortions of the production process, monetary calculation during periods of inflation�are all swept aside by assumptions that make the remaining issues mathematically tractable.
        In the writings of the New Classicists, the analytical technique introduced by Walras and extended by Friedman has been pushed to the limits. The goal of a "fully articulated artificial economy" and the insistence on the complete absence of so-called "free parameters" is easily interpreted in terms of our Venn diagram: The border separating mathematically tractable issues from all other economic issues should be sealed once and for all.⁽⁷⁾
        Modeling techniques introduced by Edmund Phelps [1970] and developed by Robert Barro [1981] require that the border guards stand elbow to elbow. The world about which they theorize consists of a number of island economies. No trade occurs between islands. There is only one commodity being supplied and demanded. The commodity is nondurable in the extreme�a service, actually, indistinguishable from the labor that renders it. Demanders possess the same information as suppliers. Technical considerations require that the service is such that one individual must render it to another. (This feature is needed to prevent the model from collapsing into a model of complete autarchy.) The full specification of such models taxes the imagination, but Barro [1981, p. 83] achieves a degree of concreteness by suggesting that we think in terms of "back-scratching" services.
        New-Classical models of this type allow for no substitutability or complementarity among goods or among factors of production; no capital and hence no heterogeneity of capital; no information flows, entrepreneurial activities, production plans, or market processes except in the most trivial senses. Yet the purpose of such models is to facilitate the analysis of monetary shocks or of alternative monetary policy regimes. (The substantive conclusions derive from a stipulated difference in the cost of acquiring global as opposed to local information about price changes.) But what significance could the implications of such models possibly have for real-world economies?
        Thomas Sargent [1987, p. 7] is aware that the techniques of New Classicism have questionable validity: "[I]n order to make general equilibrium models tractable enough for macroeconomic work, their preferences, technology, and endowments have typically been so simplified, and so much has been abstracted, that it is often difficult to take their predictions in some directions seriously." Research efforts within the New Classicist camp, however, are directed toward further extension of this modeling technique. Questions about validity are neither answered nor seriously contemplated. According to Sargent [1987, p. 7], the technique "rests on faith that insights about the laws of motion of economic aggregates can be acquired by building models of economies that are internally consistent. Such faith perseveres despite the fact that internal consistency is always purchased with simplification and abstraction."
        In the view of Robert Lucas this faith is strong enough to establish a new method of achieving understanding and a new meaning for the word "theory." Writing about economic fluctuations, Lucas [1981, p. 219] asserts that "One exhibits understanding of business cycles by constructing a model in the most literal sense: a fully articulated artificial economy which behaves through time so as to imitate closely the time series behavior of actual economies. The Keynesian macroeconomic models were the first to attain this level of explicitness and empirical accuracy; by doing so they altered the meaning of the term 'theory' to such an extent that the older business cycle theories could not really be viewed as 'theories' at all."
        The spinning continues on the superficial analogy that in Mises's judgment had been spun out too long several decades ago. Economic understanding in Mises's own view in achieved by identifying cause-and-effect relationships between individual actions in the marketplace and the economic phenomena to which they give rise. No amount of faith can transform the articulation of an artificial economy into an understanding of a real one. The mathematical modeling that characterizes New Classicist literature is not a means of achieving economic understanding but is rather a substitute for it. 

IV. Concluding Remarks
Studies of Mises and his methods and comparisons of his praxeological reasoning with the more modern econometric and mathematical modeling techniques are fruitful pursuits. Such studies, of course, provide no pat formulas for devising economic theories or for establishing their validity and relevance, but they do provide some valuable guidance.
        It has become popular to insist that no methodological taboos be issued�except for the taboo against issuing taboos. I propose as a second exception the taboo issued earlier in this paper: "Do not allow the applicability of mathematical or statistical methods to define the scope of economics." In terms of the Venn diagram depicting the overlap between mathematics and economics, the taboo translates into the imperatives: Redeploy the border guards. Accept responsibility for demonstrating that mathematically derived results have economic relevance; refrain from drawing conclusions about real-world economies that hinge critically on some assumption made for the sake of mathematical tractability.
        In one sense these imperatives are weak ones. Who could explicitly reject them and expect to maintain intellectual respectability? In another sense they are not so weak. Their implicit rejection pervades modern economic literature. The actual observance of these imperatives would require a radical�and salutary�change in the way modern economists go about their business.
 

Bibliography

Barro, Robert J., "Rational Expectations and the Role of Monetary Policy," in Barro, Money, Expectations and Business Cycles. New York: Academic Press, 1981, pp. 79-110.

Dwyer, Gerald P., Jr., "Inflation and Government Deficits," Economic Inquiry, vol. 20, no. 3 (July) 1982, pp. 315-29.

Egger, John B., "The Austrian Method," in Louis M Spadaro, ed., New Directions in Austrian Economics. Kansas City: Sheed Andrews and McMeel, Inc., 1978, pp. 19-39.

Galloway, Lowell, and Vishwa Shukla, "The Neoclassical Production Function," American Economic Review, vol. 64, no. 2 (June) 1974, pp.348-58.

Garrison, Roger W., "Waiting in Vienna," in Mario J. Rizzo, Time Uncertainty and Disequilibrium. Lexington, MA: D. C. Heath and Co., 1979, pp. 215-26.

Fischer, Stanley, "Paul Anthony Samuelson," John Eatwell, Murray Milgate and Peter Newman, eds, The New Palgrage: A Dictionary of Economics. London: Macmillan Press, 1987, vol. IV, pp. 234-41.

Granger, C. W. J., and P. Newbold, Forecasting Economic Time Series. New York: Academic Press, 1977.

Hayek, Friedrich A. "The Theory of Complex Phenomena," in Hayek, Studies in Philosophy, Politics and Economics. Chicago: University of Chicago Press, 1967, pp. 22-42.

Herron, Caroline Rand, "Economist to Economist, in English," New York Times, Sunday, September 27, 1987, sec. 3, p. 4.

Klamer, Arjo, Conversations with Economists. Totowa, NJ: Roman and Allanheld, Publishers, 1984.

Lachmann, Ludwig M., Macro-economic Thinking. Studies in Economics No. 6. Menlo Park, CA: Institute for Humane Studies, 1978.

Lucas, Robert E. Jr., Studies in Business Cycle Theory. Cambridge, MA: M.I.T. Press, 1981.

Mises, Ludwig von, Human Action, 3rd rev. ed. Chicago: Henry Regnery Company, 1966. (First edition: 1949)

Musgrave, Alan, "'Unreal Assumptions' in Economic Theory: the F-Twist Revisited," Kyklos, vol. 34, no. 3, 1981, pp. 377-87.

Phelps, Edmund S., "The New Microeconomics in Employment and Inflation Theory," in Phelps et al., Microeconomic Foundations of Employment and Inflation Theory. New York: W. W. Norton and Company, Inc., 1970, pp. 1-23.

Rothbard, Murray N. Man, Economy, and State: A Treatise on Economic Principles. Los Angeles: Nash Publishing Co., 1970.

Samuelson, Paul A., Foundations of Economic Analysis. New York: Atheneum, 1974. (Originally published in 1947)

Sargent, Thomas J., Dynamic Macroeconomic Theory. Cambridge MA: Harvard University Press, 1987.

Sims, Christopher A., "Money, Income, and Causality," American Economic Review, vol. 62, no. 4 (September) 1972, pp. 540-52.

Stigler, George J., Production and Distribution Theories. New York, Macmillan and Co., 1946.

Yeager, Leland B., "Capital Paradoxes and the Concept of Waiting," in Mario J. Rizzo, Time Uncertainty and Disequilibrium. Lexington, MA: D. C. Heath and Co., 1979, pp. 187-214.
 

Notes

* The author wishes to thank Sven Thommesen (U.C.L.A.) and Parth Shah (Auburn University) for helpful comments on an earlier draft of this paper.

1. Praxeology can be interpreted as "action logic" in which it is recognized that actions (a) transpire through time and (b) are motivated by perceived cause-and-effect relationships. In Mises' own words [1966, p. 99], "What distinguishes epistomologically the praxeological system from the logical system is precisely that it implies the categories of time and causality."

2. For an illuminating contrast between "cause and effect" and "mutual determination" in the context of production theory, see Rothbard [1970, pp. 277-80].

3. Ludwig Lachmann [1978] provides an insightful critique of this relationship. His own dissatisfaction with the neo-Ricardian theory derives from the absence of an adequate microeconomic foundation. In particular, the neo-Ricardians are in clear violation of Lachmann's second rule: "In discussing a system of action..., we are not entitled to abstract from the springs of human action, the purposes sought by individuals and the plans in which they find their expression by assuming their modus operandi to be known and therefore predictable" [1978, p. 6].

4. The mathematician in his limited role as "pattern maker" and the statistician in his similarly limited role are discussed by Hayek [1967].

5. Assumptions are often made for the sake of conceptual rather than mathematical tractability. Mises, for instance, never hesitated to invoke the ceteris paribus assumption--even when

it was clearly unrealistic. Debate in recent years about the merits of realism per se has been particularly unproductive. See Musgrave [1981] for a fruitful recasting of this methodological issue.

6. For a critical exposition of the Cambridge controversy and a methodological treatment of the specific issues, see Lachmann [1978, pp. 15-17], Yeager [1979, pp. 187-93], and Garrison [1979, pp. 221-24].

7. Arjo Klamer's conversations with Lucas, Sargent, and Townsend [Klamer, 1984] lend support to this interpretation.