Roger W. Garrison

There is much pedagogical value in applying the economist's standard analytical tools to issues about which students have a common-sense understanding. By demonstrating this point repeatedly, Steven Landsburg has become the profession's pre-eminent Armchair Economist (Landsburg, 1993). "Why Popcorn Costs More at the Movies" (pp. 157-167) may not be a critical issue in its own right, but dealing with such light-weight issues can be an effective way of teaching analytical skills.
     More recently, Landsburg (Slate, 2002) has dealt with the downright frivolous question: Why don't people walk up escalators? Or alternatively, Why don't people stand still on stairs. Landsburg's answer, which he attributes to Mark Bils, involves taking escalators and stairs to be instances of superior and inferior machines. Just as workers should spend less time with an inferior machine, people should spend less time on stairs. Well, standing still on stairs clearly violates that maxim.
     While Bils and Landsburg get points here for matching answer to question in terms of the degree of frivolity, they forgo the opportunity to showcase the economic way of thinking by applying standard indifference-curve analysis.

RESTING AND MOVING

The relevant decision, undoubtedly made subconsciously by the typical stair climber or escalator rider, involves a trade-off between "resting" and "moving." These two gerunds, then, label the vertical axis (resting) and the horizontal axis (moving) of the indifference-curve map in Figure 1. The ultimate form of resting in this context consists of standing still, which is the level of rest that defines the vertical intercept of a linear budget constraint. (A possible budget-constraint non-linearity in the case of moving walkways will be considered below.) The horizontal intercept corresponds to zero rest and has our stair climber racing as fast as possible. We should let this budget constraint be applicable only to ascending the stairs; the constraint applicable to descending would have a horizontal intercept lying further to the right. People can race down the stairs faster than they can race up them. ⁽¹⁾ In either application and except in extreme circumstances, the actual trade-off will be struck somewhere between standing still and racing as fast as possible. 
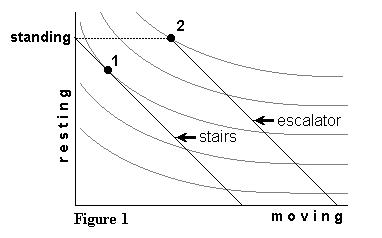     Straightforwardly, the indifference curve map shows our ascender's preferences when faced with a choice between resting more and moving faster. A tangency between the budget constraint and an indifference curve occurs at Point 1, which identifies the optimal combination of resting and moving on the stairway.
     If the stairway is replaced by an escalator, our budget constraint must be replaced as well. The new constraint has the same slope as the old one but is shifted to the right by a magnitude representing the speed of the escalator. Having the same slope simply means that walking up an escalator and walking up stairs are equally unrestful activities. (If walking up an escalator is judged to be more unrestful—because of the higher steps and less suitable rise-to-run ratio—then the budget constraint for the escalator would be a little steeper than the one for the stairs.)
     Important for application in normal circumstances is the fact that the new budget constraint is truncated at the level of rest associated with standing still. The constraint does not extend upward from that point toward the vertical axis. This is only to say that you cannot improve on the restfulness associated with standing still by walking or running backwards on the escalator. Thus, the point that represents standing still and moving at escalator speed is a potential corner solution. The preference map shows that this corner, Point 2, is in fact the optimal choice for our typical rider. 
     We see from Figure 1 that our climber-cum-rider deals with the gain offered by an escalator in conventional ways. The gain is taken partly in the form of more rest and partly in the form of more speed. The corner solution implies that some riders would actually go further in trading speed for rest at the margin if that were technologically possible. But given their actual options, they are constrained to move at escalator speed while just standing there. 
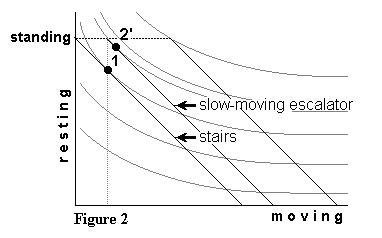     Wouldn't people be better off with escalators that allowed for tangency solutions? The general shape of the indifference curves suggests achieving a tangency would require escalators to move more slowly. Figure 2 shows the case where the escalator moves at the optimal stair-climbing speed established in Figure 1. With the potential corner solution directly above Point 1, the typical rider would not adopt that corner as a solution. To stand still on the slow-moving escalator would imply an indifference curve that is perfectly vertical between Point 1 and the corner. Most everyone would walk up—with some, presumably, ascending faster than others. Note, however, that the tangency solution (at Point 2') entails a degree of utility that is less than that associated with the corner solution in Figure 1. Riders are better off with a corner solution on a faster-moving escalator.
     Providing answers to the original inquiry (Why don't people walk up escalators?) leads us to a related question—a question that has a more satisfying answer: On what basis do escalator manufactures set the speed of their escalators? It would seem that they set the speed at a level that puts most riders at a corner solution. ⁽²⁾ With most riders standing still, the conflicts among riders are nullified. Further, the dominance of the corner solution justifies an escalator design that best accommodates standers. (The slow-moving escalator of Figure 2 should have a step height and rise-to-run ratio of a conventional stairway. That design would best accommodate the climbers.)
     Even with the faster-moving escalator of Figure 1, some people will climb. Their preferences imply a tangency solution. Some may even climb as rapidly as they would climb stairs. These people are simply taking all of the gain provided by the escalator in the form of speed and none of the gain in the form of rest. ⁽³⁾ It is probably the case that an escalator speed set so high that literally no one would walk or run up it is set so high that virtually no one would get on it. Further, we see in the following section that it is no contradiction of economic theory for some people in some circumstances to move faster up an escalator than they would move on stairs. 

TRAINS, PLANES, AND CONVENTION HOTELS

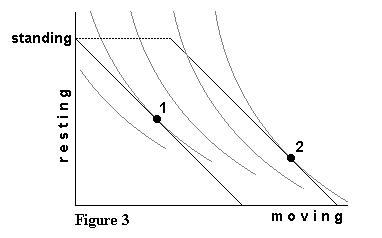
Figure 3 is identical to Figure 1 in terms of the shape and location of the budget constraints, but it differs from the earlier figure in terms of the preference map. Given the particular indifference curves of Figure 3, we get a tangency solution in which the rider actually leverages the gain provided by the escalator. As implied by a movement from Point 1 to Point 2, he runs up it, though with stairs he would only have walked up. We can easily imagine the circumstances in which these preferences are understandable. Suppose it is very much worth while to get to the next floor quickly but that if you can't get there quickly, it doesn't much matter whether you get there a little later or even later still. Train stations and airports provide circumstances where these indifference curves might apply. 
     The escalator may give the traveler just the leverage he or she needs to catch an on-time plane. But absent the escalator, all hope is lost. The stair-climber walks up the stairs at a normal pace—on the chance that the train/plane is late or to check the time table for the next departure. (Undoubtedly, some of these travelers might have run up the stairs. Still, the case in which a traveler would walk up the stairs but run up the escalator is conceivable and even plausible.) The behavior motivated by the preference map in Figure 3 is probably common in train stations and airports but rare to non-existent in convention hotels. Convention participants are not terribly concerned about missing the first few minutes of some session on the application of indifference-curve analysis. 
     Shopping malls are usually like convention hotels but are sometimes like train stations and airports. On the day after Christmas or on other special sales days, it is critical to get to the merchandise ahead of the crowd; but failing that, it will do just to see what's left over after the mad scramble. Shoppers whose preferences are more conventional—i.e., similar to the ones shown in Figure 1—might want to be put on notice that there are other shoppers among them whose preference maps are similar to the one shown in Figure 3. Possibly it would be worthwhile to create an iconic symbol that resembles the pattern of indifference curves of Figure 3 and post it near the mall entrance on sales days. The notice could serve a function similar to a posting at the beach that warns of a rip tide.
 

MOVING WALKWAYS

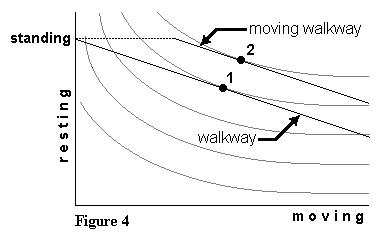An indifference-curve treatment of moving walkways would seem to be similar in all respects to our treatment of escalators. But there are critical differences. The budget constraint has a much shallower slope and possibly is non-linear near the vertical intercept, virtually precluding the kind of dominant corner solution that characterizes our analysis of escalators. Figure 4 shows indifference curves from the same preference map used in Figure 1. But the budget constraint has a slope that is considerably less than in Figure 1: On a level playing field, people can trade rest for speed on much more favorable terms. 
     The shallow slope alone makes it unlikely that a corner solution will dominate. In Figure 4, our typical rider takes advantage of a moving walkway by locating at Point 2, which constitutes a tangency solution. It is without contradiction, then, that many people (including the author) stand on an escalator 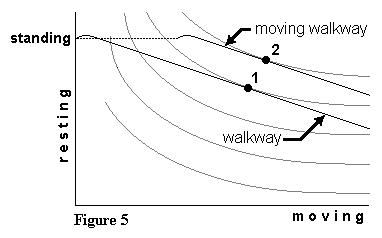but walk on a moving walkway. Making a corner solution even less likely is the fact that for many, strolling may seem more restful than standing. (Strolling around a shopping mall certainly seems less tiring than just standing in one of the stores.) If strolling is preferred to walking even on grounds of restfulness, then the budget constraint itself rises from its vertical intercept and then slopes downward at speeds beyond the stroll. As is clear in Figure 5, this kind of non-linearity would preclude a corner solution.
     Of course, some people do stand on moving walkways. Standing may even be typical for riders who have luggage or are otherwise encumbered. Others stroll for added restfulness or to avoid boredom. Still others walk, taking only part of the gain provided by the moving walkway in the form of rest, or they walk fast, leveraging the gain. Without a corner solution to fix a dominant mode of usage, measures need to be taken to deal with the variety of modes. Typically, riders are reminded by conspicuous signs or by a taped voice to stand on the right or walk on the left. Though less common (except possibly in England), this same convention can be prescribed for escalator riders. 

SUMMARY

Using indifference curve analysis to show why people stand still on escalators but walk on moving walkways helps establish the near-universal applicability of economic theory. Working with contrasting preference maps (such as those in Figures 1 and 3) to deal with an issue where the student's own intuition is fully in play may help the student to read indifference curves in less intuitive cases. And challenging the students to apply basic economic tools to similarly frivolous issues can result in fun and even learning. 
     The only down side to exposing students to this armchair view of escalators is that they may never again be able to ride an airport escalator without thinking of indifference-curve analysis. 

REFERENCES

Landsburg, S. E. (2002). Everyday Economics: "Why do you walk up staircases but not up escalators? Slate (http://slate.msm.com), August 28.

Landsburg, S. E. (1993). The Armchair Economist: Economics and Everyday Life. New York: The Free Press.

NOTES

1. One of my colleagues whose armchair is much newer than my own claims that she can go up the stairs (taking three steps at a time) faster than she can go down (having to use every step).

2. Actually polling the manufactures of escalators on this question, of course, would violate the spirit of armchair theorizing. In any case, we can claim they behave as if they have a corner solution in mind.

3. According to Landsburg (2002), the Bils-Landsburg argument "proves...that even if you choose to walk on the escalator, you should always walk even faster on the stairs" (emphasis added). The "always," it turns out, makes their statement too strong.